Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

На рисунке изображен график функции y = f(x), определённой на интервале (-11;2).
Найдите  количество точек, в которых производная функции f(x) равна 0.

Если производная функции равна нулю, то угловой коэффициент касательной, проведённой
к графику функции в этой точке (или тангенс угла наклона касательной
к положительному направлению оси ОХ) тоже равен нулю.



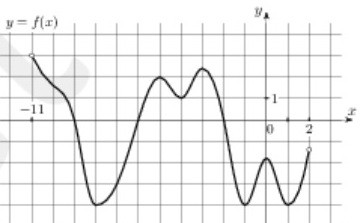
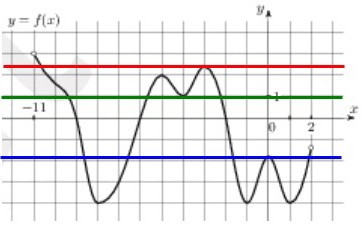Иначе говоря, касательная к графику функции в этой точке параллельна оси ОХ.
Примеры таких касательных приведены на рисунке выше.



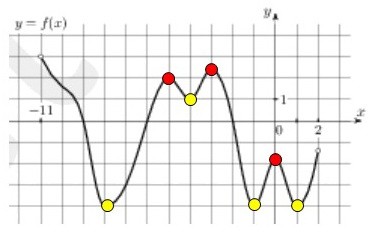Осталось посчитать, сколько горизонтальных касательных можно провести.
На графике ровно семь соответствующих точек (их называют критическими).
Ответ: 7

Заметим заодно, что все эти точки являются и точками экстремума функции,
среди которых отличают точки максимума (красные) и минимума (жёлтые).

Автор: Ольга Себедаш             Просмотров: 165089