Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Ребра тетраэдра равны 1. Найдите  площадь  сечения, проходящего
через середины четырех его ребер.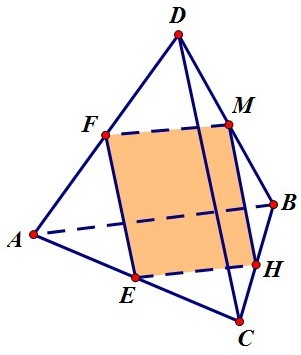

Если интуиция подсказывает вам сразу, что сечением является квадрат,
то остаётся лишь найти его сторону, и площадь будет у вас в кармане!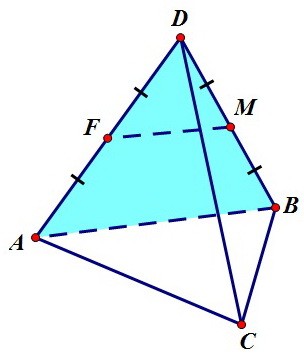



Рассмотрим, например, треугольник ADB, в котором одна из сторон
квадрата является средней линией, а значит, FM = 0,5 · AB = 0,5.
Найти теперь площадь квадрата - дело техники: S = 0,5 · 0,5 = 0,25.

Ответ: 0,25

И всё же, несмотря на то, что ответ нами получен вроде бы "в рамках правил",
решим задачу более честно, доказав предварительно, что перед нами квадрат.
Сначала покажем параллельность противоположных сторон данного сечения.



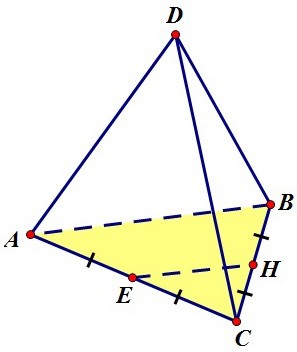Средняя линия ЕН треугольника АВС параллельна основанию АВ так же, как
средняя линия FM параллельна тому же отрезку АВ (на предыдущем рисунке).
По признаку параллельности прямых стороны ЕН и FM параллельны друг другу.
Аналогично доказывается параллельность другой пары сторон сечения.

Достаточно ли этих рассуждений теперь? Нет. Пока перед нами только ромб.
Требуется доказать, например, что угол между соседними сторонами прямой.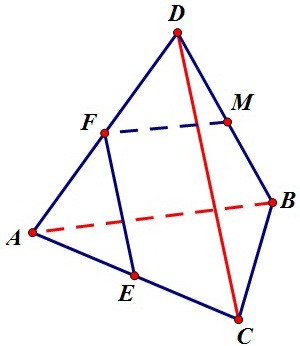



Для этого достаточно доказать перпендикулярность рёбер АВ и DС тетраэдра.
После этого мы учтём параллельность прямых FE и DC, а также FM и AB.
Как доказать перпендикулярность красных рёбер? Рассмотрим плоскость CDT.



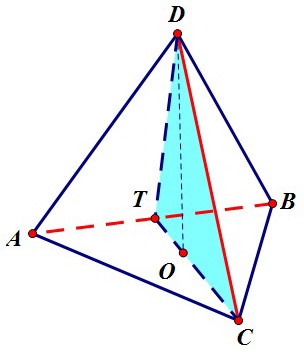Плоскость проходит через ребро CD и высоту DO тетраэдра. Точка О лежит
на медиане СТ равностороннего треугольника АВС, т.е. точка Т - середина АВ.
Медианы СТ и DT треугольников являются и высотами, т.е. СТ ⊥ АВ и DT ⊥ АВ.
Это значит, что прямая АВ перпендикулярна плоскости CDT по признаку
перпендикулярности прямой и плоскости, а значит, и прямой CD, лежащей
в этой плоскости, по определению перпендикулярности прямой и плоскости.

Вот теперь наше сечение из ромба превратилось в настоящий квадрат.

Автор: Ольга Себедаш             Просмотров: 78400