Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
14(C2). Часть 2. Находим угол между стороной и диагональю сечения (вар. 42)
Комментарии к этой задаче: Комментарий добавил(а): Алла основное определить положение точки S, но оно никак не оговаривается. Комментарий добавил(а): egetrener Алла, выше есть ссылочка на первую часть. Это часть номер два. Комментарий добавил(а): Алла Спасибо. Комментарий добавил(а): Радиф Галиевич Наверное, лучше и не бывает... Комментарий добавил(а): тамара Ольга Игоревна,спасибо за решение. Красота. Комментарий добавил(а): Владимир Ольга Игоревна! Спасибо большое за великолепное объяснение. Но не пойму, почему в заголовке "угол между скрещивающимися прямыми? Комментарий добавил(а): egetrener Владимир, спасибо, поправлю. Комментарий добавил(а): Флюра Никак не могу понять, почему АМ=2/3? Комментарий добавил(а): Флюра Неужели такую сложную задачу под силу решить простому школьнику? И которая оценивается всего в 2 балла?! Издевательство. А Вам Ольга большое спасибо за оригинальное решение. Вот почему при разложении векторов по базисам Вы взяли именно число 30? а можно без этого числа прорешать? пусть даже с дробями. Спасибо. Комментарий добавил(а): egetrener Флюра, Вы спрашиваете, почему CQ=2/3·CB? По условию. Число 30 взяла,т.к. оно делится на 2, на 3 и на 5. Не люблю дроби) Конечно, можно решать и с дробями. Комментарий добавил(а): Флюра Спасибо за ответ. Но я спросила почему АМ = 2/3? То что СQ = 2/3CВ-это я знаю! Комментарий добавил(а): egetrener Флюра, но у меня нет точки М. Комментарий добавил(а): GVS Уважаемая Ольга Игоревна! Может быть, ребро тетраэдра равно не шести, а тридцати? Комментарий добавил(а): Рубен Пожалуйста, объясните слова: "При этом заметим, что i·j = i·k = j·k = 0,5, i2 = j2 = k2 = 1." На чем основаны эти умозаключения? Комментарий добавил(а): Ольга Себедаш Рубен, почитайте о скалярном произведении векторов. Комментарий добавил(а): Наталья Н Уважаемая Ольга Игоревна! Подскажите, пожалуйста, сколько времени у Вас заняло это решение. Комментарий добавил(а): Ольга Себедаш Наталья Н., само оформление здесь, на сайте, заняло много времени, конечно. Но решение... не помню уже) Кажется, не очень Комментарий добавил(а): Марьяна а без векторов никак нельзя ?... Комментарий добавил(а): Добавить Ваш комментарий: |
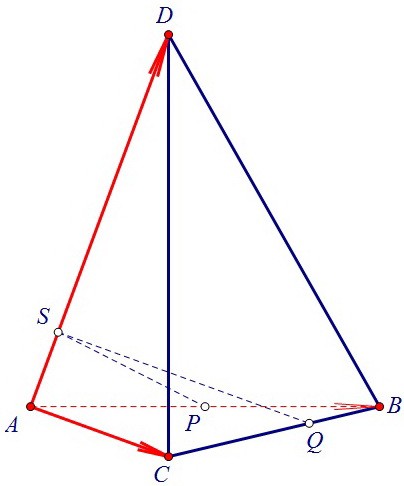Чтобы избежать дробей в вычислениях и учитывая положение точек S, P и Q,
введём базисные векторы i, j и k, такие что AC = 30·i, AB = 30·j и AD = 30·k.
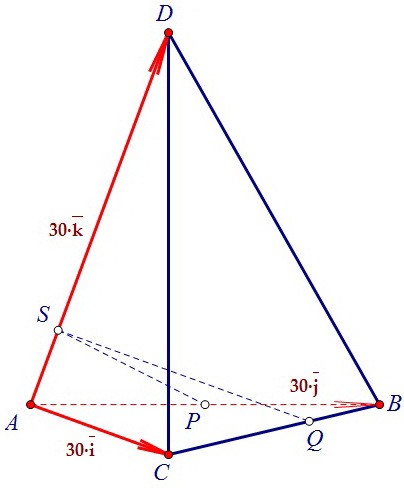Выразим через базисные векторы вектор SP: SP = SA + AP.
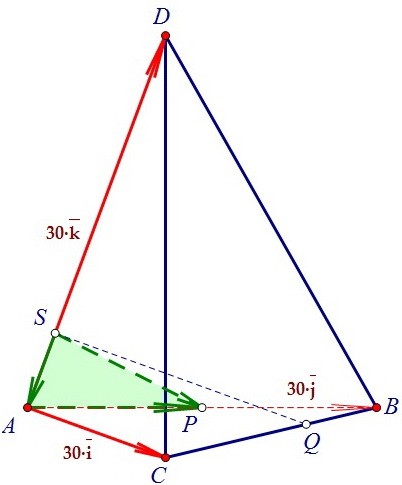Получим, что SP = -6·k + 15·j = 15·j - 6·k.
Выразим через базисные векторы вектор SQ: SQ = SA + AC + CQ.
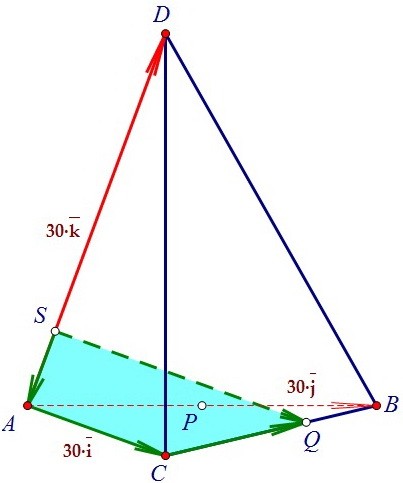Получим, что SQ = -6·k + 30·i + 2/3·CB.
SQ = -6·k + 30·i + 2/3·(-30·i + 30·j) = 10·i + 20·j - 6·k.
Выпишем результаты здесь. SP = 15·j - 6·k; SQ = 10·i + 20·j - 6·k.
Вспомним, что угол между векторами находится следующим образом:
