Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Отрезки секущих и касательная образуют геометрическую прогрессию (вар. 42)
Комментарии к этой задаче: Комментарий добавил(а): светлана Какая Вы умница! Комментарий добавил(а): VictorSh Спасибо,Ольга Игоревна! Все просто замечательно!!! Отличное решение! Комментарий добавил(а): Радиф Галиевич Гениально! Комментарий добавил(а): Тамара Александровна Здорово! Очень красивое решение! Большое спасибо, Ольга Игоревна! Комментарий добавил(а): Флюра Ольга Игоревна! не голова, а дом советов!! ПРОСТО, ДОСТУПНО, ОРИГИНАЛЬНО!!! Спасибо большое! Мне показалось, что эта задача проще, чем С2! Комментарий добавил(а): Елена Ольга Игоревна, огромное спасибо! Все Ваши решения прекрасны. Комментарий добавил(а): Нина Федоровна Спасибо за решение! Очень красиво и четко изложено! Комментарий добавил(а): Михаил Н. Ольга Игоревна. "Разгадывать секрет" для того, чтобы решить эту задачу, как утверждаете Вы, вовсе не требуется. Тот факт, что расстояние между А и С не зависит от положения точка К при условии равенства КС и KF, интересный, но для данной задачи он не нужен и только усложняет процесс решения. Треугольник ACF вписанный, F известный, больше ничего не надо. Добавить Ваш комментарий: |

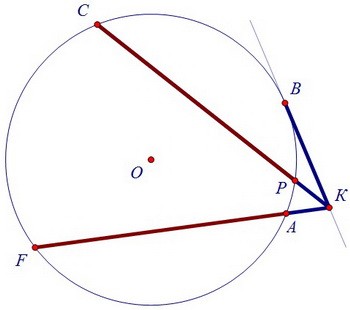 Рассмотрим отрезки КР и КС другой секущей и будем рассуждать так же:
Рассмотрим отрезки КР и КС другой секущей и будем рассуждать так же:
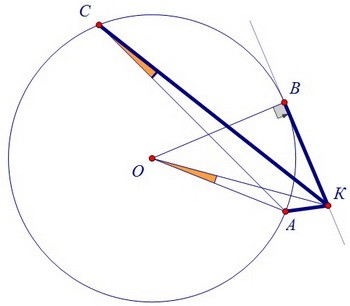
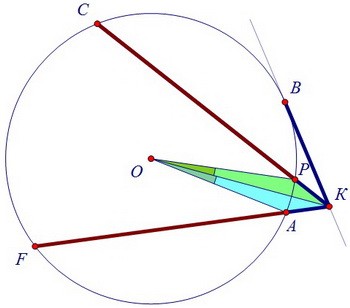 Закрашенные треугольники равны по трём сторонам. И значит, ∠АОК = ∠РОК.
Центральный угол АОР и вписанный угол АСР опираются на одну дугу АР.
Закрашенные треугольники равны по трём сторонам. И значит, ∠АОК = ∠РОК.
Центральный угол АОР и вписанный угол АСР опираются на одну дугу АР.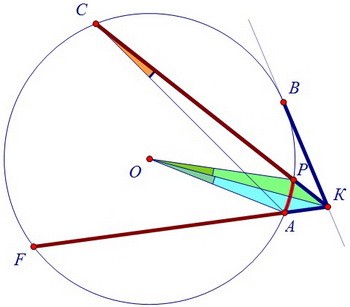 ∠АОР = 2·∠АСР, а ∠АОК = 0,5·∠АОР = ∠АСК, что и требовалось доказать.
∠АОР = 2·∠АСР, а ∠АОК = 0,5·∠АОР = ∠АСК, что и требовалось доказать.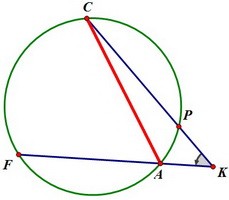
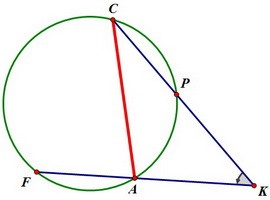
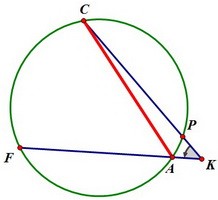 В чём тут секрет? Разгадав его, мы и решим задачу. Прежде чем читать, подумайте!
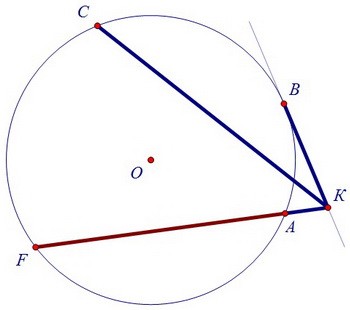
Так как треугольник СКF равнобедренный, то угол К однозначно определяет угол F.
В чём тут секрет? Разгадав его, мы и решим задачу. Прежде чем читать, подумайте!
Так как треугольник СКF равнобедренный, то угол К однозначно определяет угол F.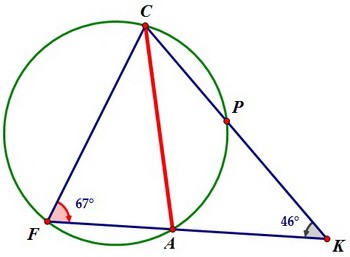 А радиус окружности и вписанный угол задают хорду, на которую угол опирается.
А радиус окружности и вписанный угол задают хорду, на которую угол опирается.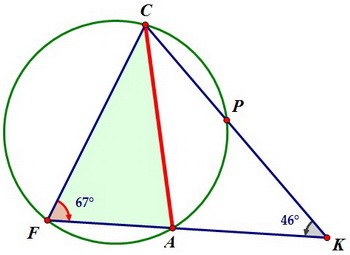 Дело всё в том, что треугольник АСF вписан в окружность, и по теореме синусов
Дело всё в том, что треугольник АСF вписан в окружность, и по теореме синусов