|
5. Показательное уравнение с разными основаниями и равными показателями (вар. 45)
|
Найдите корень уравнения
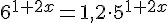
Намётанный взгляд сразу приметит следующее: если показателей не станет совсем,
то равенство будет выполняться: 6 = 1,2 · 5. Показатель на самом деле не исчезает,а обращается в единицу. 2х + 1 = 1; 2х = 0; х = 0. Корень уравнения найден, х = 0.
Однако, это не очень честный путь. Теоретически у уравнения могут быть другие корни.
Если слева и справа стоят степени с разными основаниями, но равными показателями,
то хорошо работает следующий приём: обе части уравнения делим на одну из степеней.
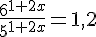Воспользуемся свойством деления степеней с равными показателями: an : bn = (a : b)n.
^{1+2x}=\frac{6}{5})
^{1+2x}=(\frac{6}{5})^1)
Справа десятичную дробь 1,2 представили в виде неправильной обыкновенной.
Степени равны, основания равны, осталось приравнять показатели степеней:
1 + 2х = 1
2х = 0
х = 0
Ответ: 0 Автор: Ольга Себедаш Просмотров: 9665
|
|
