Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной 
около цилиндра, радиус основания которого равен √27, а высота равна 1.

Площадь боковой поверхности правильной шестиугольной призмы состоит из площадей
шести равных прямоугольников - боковых граней призмы: S_бок. = 6 · S_{прямоуг.}



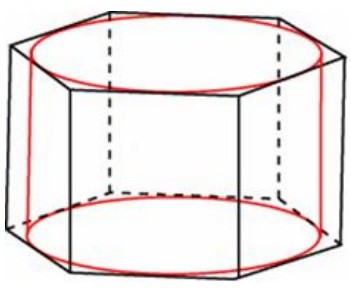
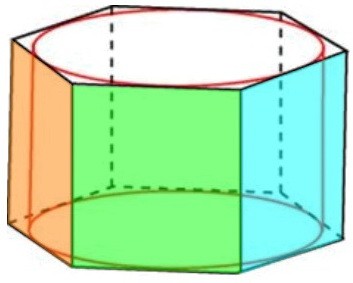Одна из сторон прямоугольника равна высоте вписанного цилиндра и дана по условию.
Вторую сторону требуется найти. Иначе говоря, нам надо найти сторону шестиугольника.
Дан радиус вписанного цилиндра, т.е. радиус вписанной в шестиугольник окружности.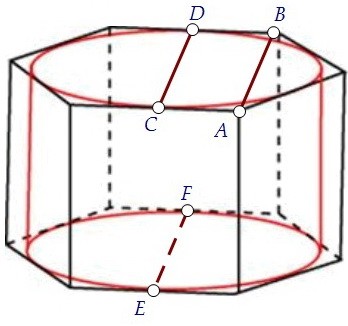



Диаметр этой окружности можно изобразить по-разному. Удобнее иметь дело с отрезком АВ.
Треугольник АВР - равнобедренный (РВ = РА) с углом при вершине 120°. Основание
в таком треугольнике в √3 раз больше боковой стороны, что полезно знать.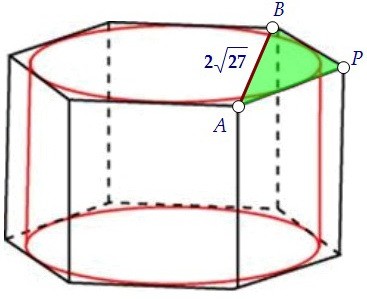



Для подтверждения этого факта можно использовать теорему косинусов для стороны АВ:

АВ² = а² + а² - 2 · а · а · cos120°
АВ² = 2а² - 2а² · (-0,5)
АВ² = 2а² + а²
АВ² = 3а²
AB = a√3
2√27 = a√3
6√3 = a√3
a = 6

Таким образом, одна сторона прямоугольника равна шести, вторая сторона равна единице.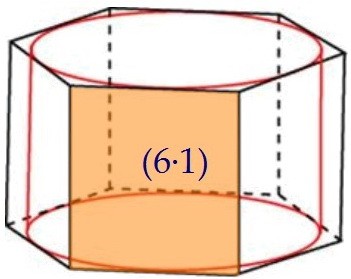



Площадь боковой грани равна 6 · 1 = 6, площадь боковой поверхности равна 6 · 6 = 36.

Ответ: 36

Автор: Ольга Себедаш             Просмотров: 77028