Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Два бегуна одновременно стартовали в одном направлении из одного и того же
места круговой трассы. Спустя один час, когда одному из них оставался 1 км
до окончания первого круга, ему сообщили, что второй бегун прошел первый
круг 5 минут назад. Найдите скорость первого бегуна, если известно,
что она на 2 км/ч меньше скорости второго.

Круговая трасса или прямая - в данной задаче это никакого значения не имеет.



Остановим время через час после старта. Интересно, что пути, которые бегуны
пробежали за час, численно равны их скоростям. Воспользуемся этим фактом.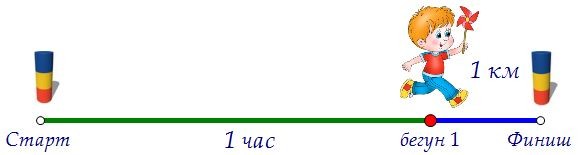



Из условия следует, что второй бегун пробежал за один час на два км больше первого.
Но первому до финиша остался 1 км. Значит, второй отбежал от финиша на тот же 1 км.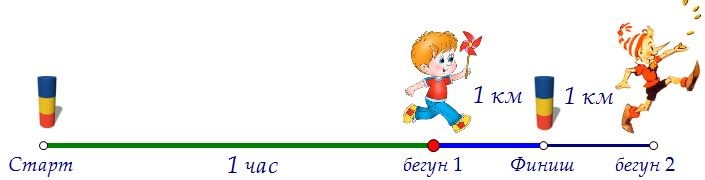



И этот самый километр второй бегун преодолел за пять минут, как сообщили первому.
Найти скорость второго теперь просто. Если за 5 минут он пробегает 1 километр, то
за час он пробежит в 12 раз больше, т.е. 12 километров. Его скорость 12 км/час.
Ну а скорость первого бегуна на 2 км/час меньше, т.е. равна 10 км/час.

Ответ: 10 км/час

Решим задачу с помощью уравнения, обозначив соответственно скорости бегунов.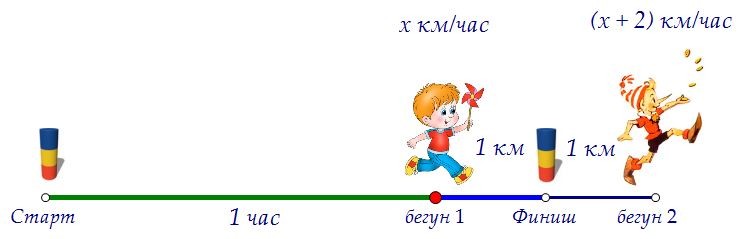



Путь, который за 55 минут пробежал второй (от старта до финиша), на 1 км больше,
чем путь, который пробежал за час первый (он километр не добежал до финиша).



Отсюда найдём, что х = 10.

Автор: Ольга Себедаш             Просмотров: 35387