Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

На продолжении ребра ST за точку Т правильной четырехугольной пирамиды SPQRT
с вершиной S взята точка В так, что расстояние от этой точки до плоскости SPQ
равно . Найти длину отрезка ВТ, если QR = 12, SR = 10.

Продлив ребро ST, продлим и другие боковые рёбра на то же самое расстояние.



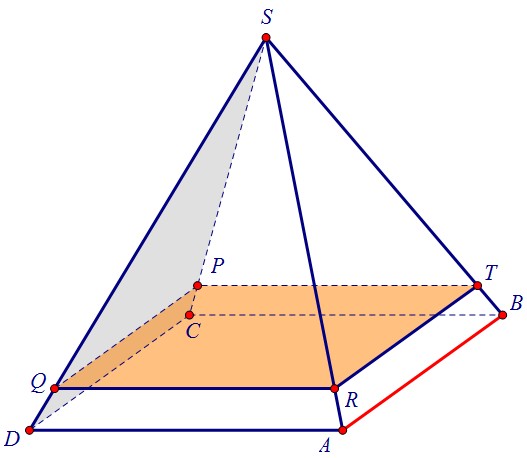Новая пирамида подобна старой. Вот узнать бы коэффициент подобия пирамид!
Чтобы найти расстояние от т. В до плоскости SPQ, достаточно найти расстояние
от прямой АВ до этой плоскости, т.к. АВ || SPQ. А для этого достаточно найти
расстояние от любой точки прямой АВ до плоскости. Возьмём М - середину АВ.



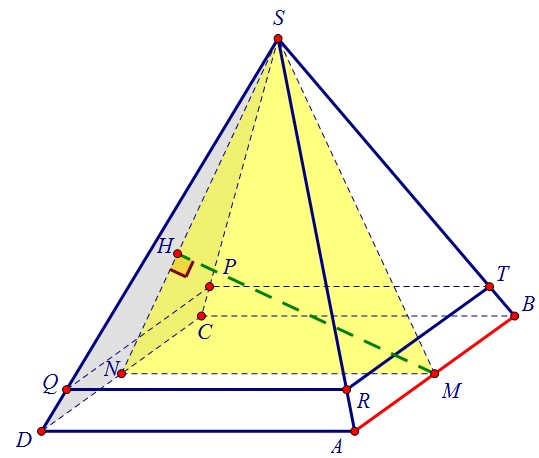Плоскости MNS и SPQ перпендикулярны и пересекаются по прямой SN. Поэтому,
чтобы провести перпендикуляр из точки М к плоскости SPQ, достаточно провести
его к прямой SN. Отрезок МН и есть данное в условии расстояние, МН = .

Найти бы теперь аналогичное расстояние от середины RT до плоскости SPQ
в маленькой пирамиде SPQRT. Тогда мы бы узнали и коэффициент подобия.



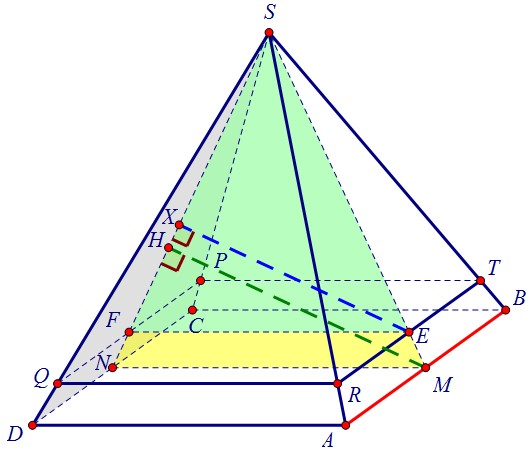Воспользуемся тем, что сторона основания и боковое ребро пирамиды SPQRT нам даны.



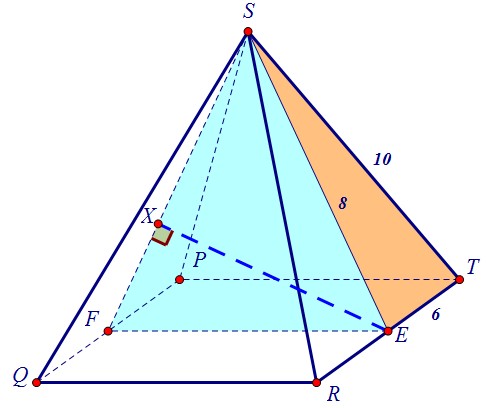Сначала из треугольника STE найдём SЕ - сторону равнобедренного треугольника FSE.
Затем из треугольника ESL найдём SL - высоту равнобедренного треугольника FSE.



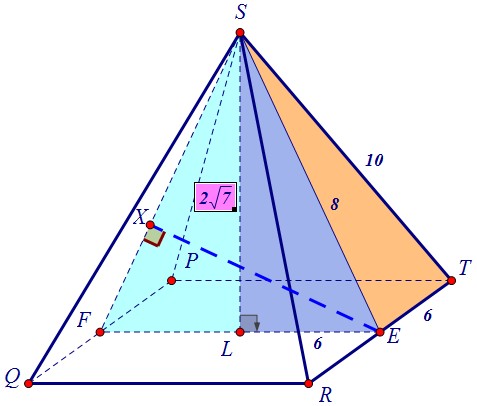Осталось найти высоту треугольника FSE, проведённую к стороне FS. Приём известен:
FE·SL = SF·EX
12·2√7 = 8·EX
EX = 3√7
Заметим, что найденное расстояние в полтора раза меньше данного в условии .



Таким образом, коэффициент подобия пирамид равен 1,5.
MH = 1,5·EX
SM = 1,5·SE
SB = 1,5·ST = 1,5·10 = 15
BT = SB - ST = 15 - 10 = 5

Ответ: 5

===========================================
Внимательный читатель заметит, безусловно, что числа в задаче таковы, что
треугольники FSE и NSM тупоугольные, и значит, высоты EX и MH попадают
на продолжение боковых сторон. Суть идеи и решения от этого не меняется.

Автор: Ольга Себедаш             Просмотров: 14659