|
Найти все а, при которых уравнение имеет единственное решение.cos2(ax) + cosx = 2(cos(ax) + cosx - 1)
При решении задач с такой формулировкой обычно хорошо работает приём: --- Замечаем, что все слагаемые уравнения чётны относительно х.
--- Это значит, что если (t) корень уравнения, то (-t) тоже корень.
--- Т.к. решение должно быть единственным, то это решение 0.
--- Находим значения а, при которых число 0 является корнем.
--- Проверяем, есть ли при найденных а ещё и другие корни.
Приём хорош тем, что отсекает сразу почти все значения параметра а,
оставляя пару-тройку претендентов, которые подвергаются проверке.
В нашем случае приём не работает. 0 - корень уравнения при всех а.========================================
Пойдём тогда другим путём - просто начнём решать данное уравнение:
cos2(ax) + cosx = 2(cos(ax) + cosx - 1)
cos2(ax) - 2cos(аx) = cosx - 2
cos2(ax) - 2cos(аx) + 1 = cosx - 1
(cos(аx) - 1)2 = cosx - 1
Левая часть неотрицательна, значит, такой же должна быть и правая.
Но положительной правая быть не может (cosx ≥ 1), значит, справа 0.
Тогда и левая часть равна нулю, т.е. обе части принимают значение 0.
 & = & 1 \\
cosx & = & 1 \\
\end{array}
\right. )
Чтобы система имела решения, должно выполняться равенство:
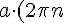}=2{\pi}m)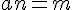 
Число 0 является корнем при любых значениях а. Рассмотрим n ≠ 0.Наша цель сейчас - найти все корни уравнения (в т.ч. ненулевые).
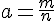Найденное значение а является рациональным, т.к. m и n - целые числа.
При этом значении параметра исходное уравнение имеет серию корней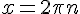 
При всех остальных а, т.е. иррациональных, уравнение имеет единственный корень х = 0.Ответ: а - иррациональное Автор: Ольга Себедаш Просмотров: 8130
|
