16(C4). Прямая p параллельна основаниям BC и AD трапеции ABCD (вар. 88)
|
Прямая p, параллельная основаниям BC и AD трапеции ABCD, пересекает прямые AB, AC, BD и CD в точках E, F, G и H соответственно, причём EF = FG.
а) Докажите, что точки пересечения прямой p с диагоналями AC и BD делят отрезок EН на три равных части;
б) Найдите EF, если BC = 3, AD = 4.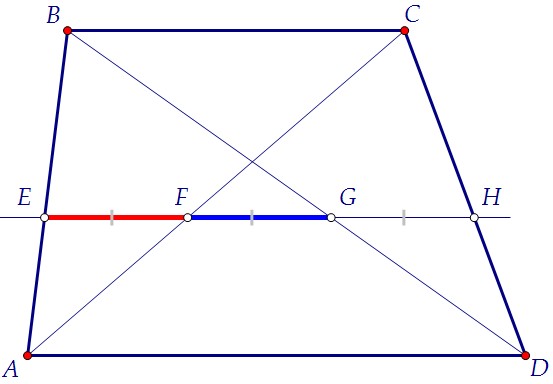 Отрезки EF и FG равны по условию. Интересно, что отрезки EF и GН тоже равны.
Отрезки EF и FG равны по условию. Интересно, что отрезки EF и GН тоже равны. 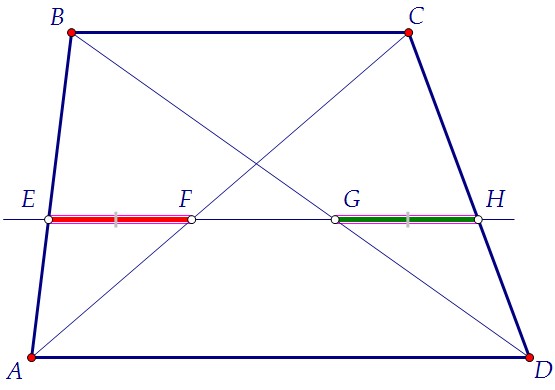 Почему? Всё очень просто следует из подобия треугольников.
1) ΔEAF и ΔBAC подобны
Почему? Всё очень просто следует из подобия треугольников.
1) ΔEAF и ΔBAC подобны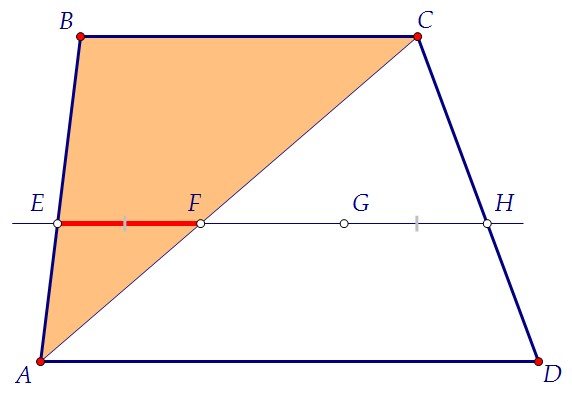 EF : BC = AE : AB2) ΔEBG и ΔABD подобны EF : BC = AE : AB2) ΔEBG и ΔABD подобны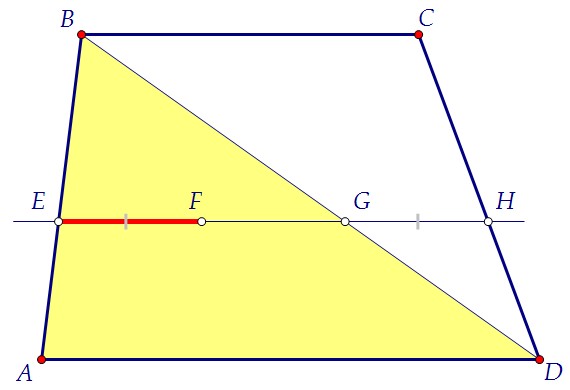 AE : AB = DG : DB3) ΔDGH и ΔDBC подобны AE : AB = DG : DB3) ΔDGH и ΔDBC подобны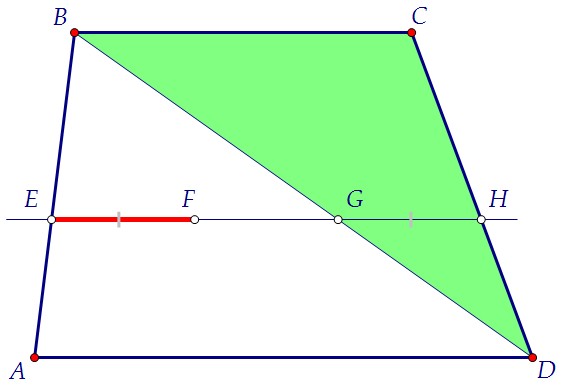 DG : DB = GH : BCОтсюда EF : BC = GH : BC и значит, EF = GHТаким образом, пункт а) доказан. EF = FG = GH===========================================Неизвестный отрезок найдём, тоже используя подобие треугольников.1) ΔEAF и ΔBAC подобны DG : DB = GH : BCОтсюда EF : BC = GH : BC и значит, EF = GHТаким образом, пункт а) доказан. EF = FG = GH===========================================Неизвестный отрезок найдём, тоже используя подобие треугольников.1) ΔEAF и ΔBAC подобны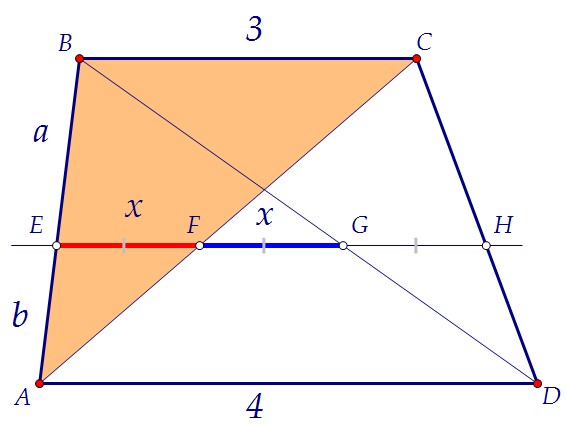 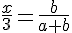 2) ΔEBG и ΔABD подобны 2) ΔEBG и ΔABD подобны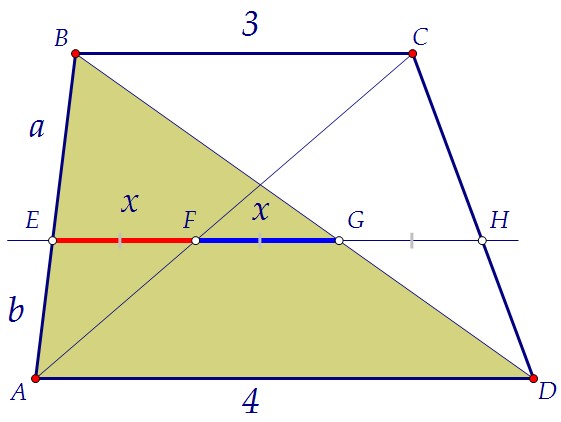 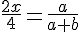 Сложим получившиеся равенства: Сложим получившиеся равенства: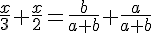 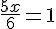 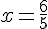 Ответ: 1,2 Ответ: 1,2 Автор: Ольга Себедаш Просмотров: 13002
|
Интересует вопрос. Почему в соотношениях сторон подобных треугольников EBG и ABD Вы берете отношение AE:AB=DG:DB, а не EB:AB=BG:DB?
Вообще то ответ должен быть 12
Аня, ну как 12 может быть? Больше обоих оснований?

 Отрезки EF и FG равны по условию. Интересно, что отрезки EF и GН тоже равны.
Отрезки EF и FG равны по условию. Интересно, что отрезки EF и GН тоже равны.  Почему? Всё очень просто следует из подобия треугольников.
1) ΔEAF и ΔBAC подобны
Почему? Всё очень просто следует из подобия треугольников.
1) ΔEAF и ΔBAC подобны EF : BC = AE : AB2) ΔEBG и ΔABD подобны
EF : BC = AE : AB2) ΔEBG и ΔABD подобны AE : AB = DG : DB3) ΔDGH и ΔDBC подобны
AE : AB = DG : DB3) ΔDGH и ΔDBC подобны DG : DB = GH : BCОтсюда EF : BC = GH : BC и значит, EF = GHТаким образом, пункт а) доказан. EF = FG = GH===========================================Неизвестный отрезок найдём, тоже используя подобие треугольников.1) ΔEAF и ΔBAC подобны
DG : DB = GH : BCОтсюда EF : BC = GH : BC и значит, EF = GHТаким образом, пункт а) доказан. EF = FG = GH===========================================Неизвестный отрезок найдём, тоже используя подобие треугольников.1) ΔEAF и ΔBAC подобны
