16(C4). Биссектриса угла А трапеции пересекает сторону СD в ее середине (вар. 93)
|
В трапеции АВСD ВС и АD – основания. Биссектриса угла А пересекает сторону СD в ее середине – точке Р.
а) Докажите, что ВР – биссектриса угла АВС.
б) Найдите площадь трапеции АВСD, если известно, что АР = 8, ВР = 6.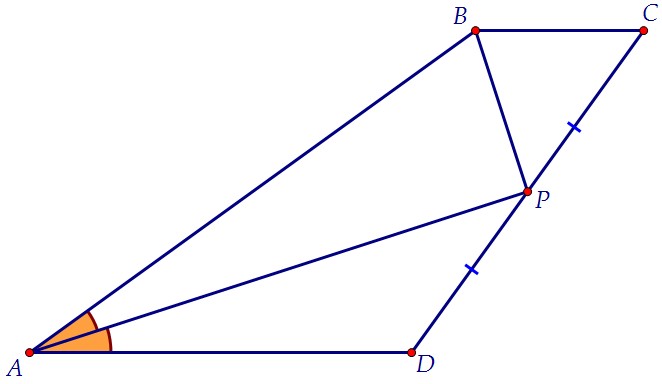 Продолжим ВР до пересечения с лучом AD, точку пересечения обозначим F.Треугольники ВРС и FPD равны по стороне и двум прилежащим к ней углам.
Продолжим ВР до пересечения с лучом AD, точку пересечения обозначим F.Треугольники ВРС и FPD равны по стороне и двум прилежащим к ней углам.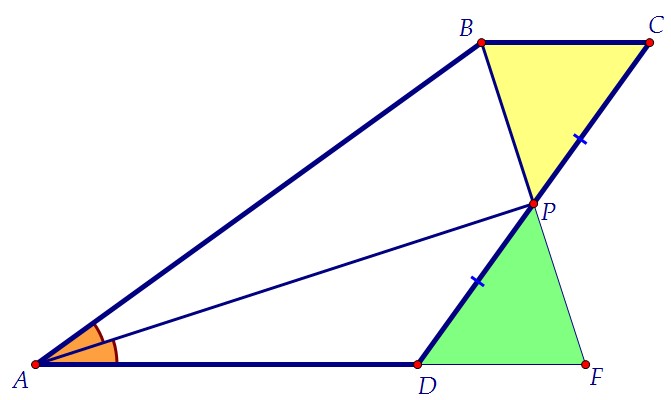 Следовательно, ВР и РF равны как соответствующие. В треугольнике ABF
медиана является биссектрисой, значит, треугольник ABF равнобедренный.
Следовательно, ВР и РF равны как соответствующие. В треугольнике ABF
медиана является биссектрисой, значит, треугольник ABF равнобедренный.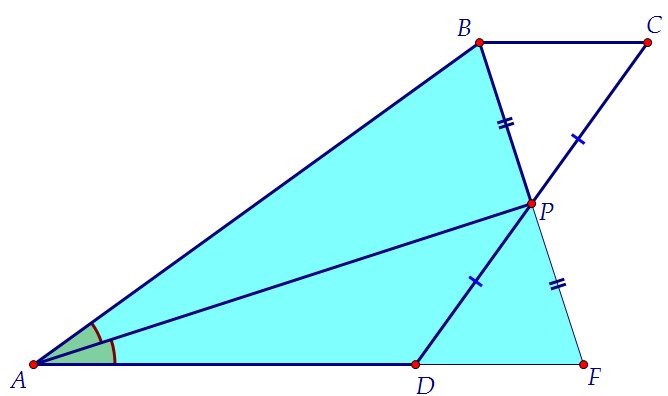 У равнобедренного треугольника по его свойству углы при основании равны, ∠1 = ∠2.
У равнобедренного треугольника по его свойству углы при основании равны, ∠1 = ∠2.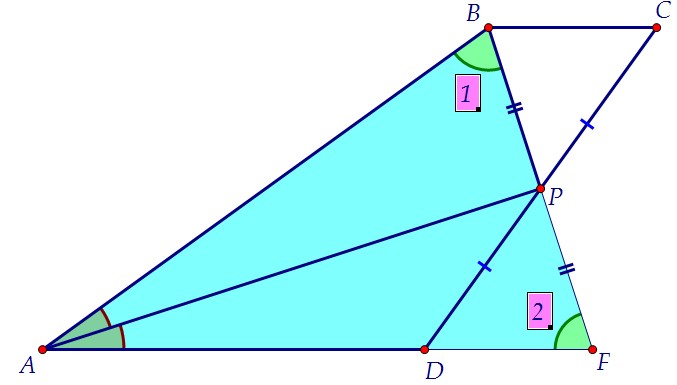 Внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей BF тоже равны, ∠2 = ∠3. Следовательно, ∠1 = ∠3, и значит, ВР – биссектриса угла АВС.
Внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей BF тоже равны, ∠2 = ∠3. Следовательно, ∠1 = ∠3, и значит, ВР – биссектриса угла АВС.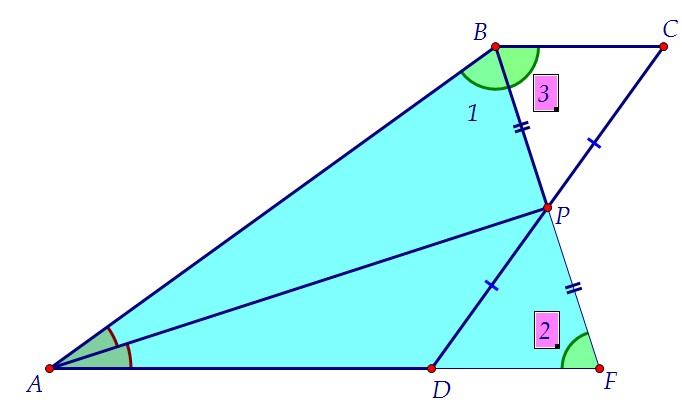 Из уже доказанного равенства треугольников ВРС и FPD следует, что площадьтрапеции АВСD равна площади равнобедренного треугольника ABF.
Из уже доказанного равенства треугольников ВРС и FPD следует, что площадьтрапеции АВСD равна площади равнобедренного треугольника ABF.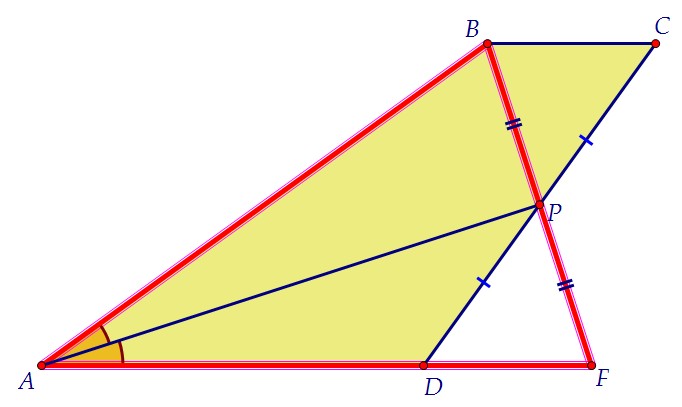 Площадь треуг. ABF равна в свою очередь удвоенной площади треугольника АВР.
Треугольник АВР прямоугольный (медиана равнобедренного треугольника ABF является его высотой), катеты его даны по условию, площадь ищется просто.
Площадь треуг. ABF равна в свою очередь удвоенной площади треугольника АВР.
Треугольник АВР прямоугольный (медиана равнобедренного треугольника ABF является его высотой), катеты его даны по условию, площадь ищется просто.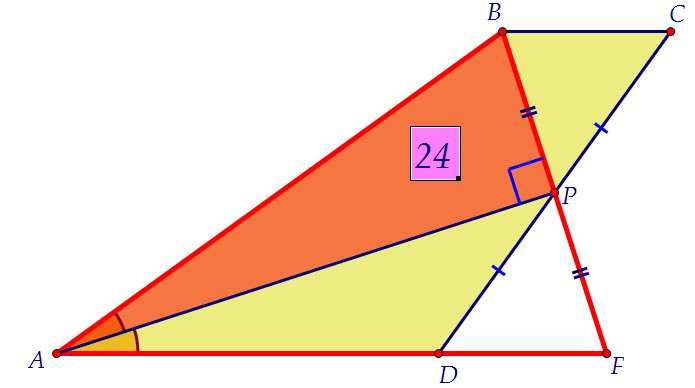 Ответ: 48 Ответ: 48 Автор: Ольга Себедаш Просмотров: 11420
|
Ольга Игоревна,спасибо за ваши уроки.Вы всё так толково и понятно объясняете.Дай бог вам здоровья! С большим уважением , Лика.
Спасибо за хорошее объяснение.Эти задачи решать всего труднее.С вашей помощью думаю научусь.С огромным уважением к вашему профессионализму.

 Продолжим ВР до пересечения с лучом AD, точку пересечения обозначим F.Треугольники ВРС и FPD равны по стороне и двум прилежащим к ней углам.
Продолжим ВР до пересечения с лучом AD, точку пересечения обозначим F.Треугольники ВРС и FPD равны по стороне и двум прилежащим к ней углам. Следовательно, ВР и РF равны как соответствующие. В треугольнике ABF
медиана является биссектрисой, значит, треугольник ABF равнобедренный.
Следовательно, ВР и РF равны как соответствующие. В треугольнике ABF
медиана является биссектрисой, значит, треугольник ABF равнобедренный. У равнобедренного треугольника по его свойству углы при основании равны, ∠1 = ∠2.
У равнобедренного треугольника по его свойству углы при основании равны, ∠1 = ∠2. Внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей BF тоже равны, ∠2 = ∠3. Следовательно, ∠1 = ∠3, и значит, ВР – биссектриса угла АВС.
Внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей BF тоже равны, ∠2 = ∠3. Следовательно, ∠1 = ∠3, и значит, ВР – биссектриса угла АВС. Из уже доказанного равенства треугольников ВРС и FPD следует, что площадьтрапеции АВСD равна площади равнобедренного треугольника ABF.
Из уже доказанного равенства треугольников ВРС и FPD следует, что площадьтрапеции АВСD равна площади равнобедренного треугольника ABF. Площадь треуг. ABF равна в свою очередь удвоенной площади треугольника АВР.
Треугольник АВР прямоугольный (медиана равнобедренного треугольника ABF является его высотой), катеты его даны по условию, площадь ищется просто.
Площадь треуг. ABF равна в свою очередь удвоенной площади треугольника АВР.
Треугольник АВР прямоугольный (медиана равнобедренного треугольника ABF является его высотой), катеты его даны по условию, площадь ищется просто. Ответ: 48
Ответ: 48