Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
19(C6). Докажите, что число 1111111.....2.....1111111 составное (вар. 105)
Комментарии к этой задаче: Комментарий добавил(а): Neooreale Добавить Ваш комментарий: |
========================
а) Заданное число получается интересным образом
121 = 110 + 11 = 11·10 + 11 = 11(10 + 1)
11211 = 11100 + 111 = 111·100 + 111 = 111(100 + 1)
1112111 = 1111000 + 1111 = 1111·1000 + 1111 = 1111(1000 + 1)
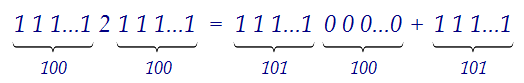
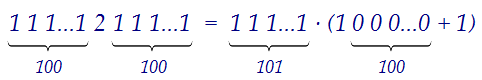Таким образом, доказано, что число в пункте а) составное.========================
б) Заметим, что показатель степени числа 2 делится на три, так как
сумма цифр показателя равна (1 + 2)·100 = 300 и делится на три.
Итак, показатель можно представить как 3n, где n натуральное.23n + 1 = (2n + 1)(4n - 2n + 1)
Таким образом, доказано, что число в пункте б) составное.========================
Попробуем поиграть с маленькими числами:
1122 = 1100 + 22 = 11(100 + 2) = 11(99 + 3) = 11·3(33 + 1) = 33(33 + 1)
111222 = 111(1000 + 2) = 111(999 + 3) = 111·3(333 + 1) = 333(333 + 1)Ну а теперь поиграем с данным числом: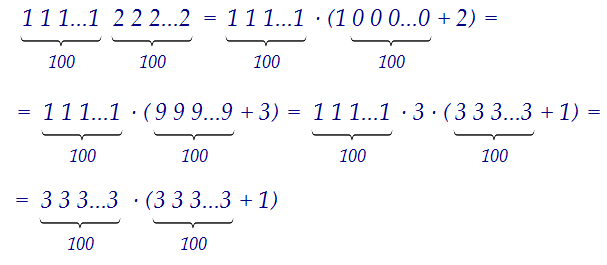
Утверждение в) доказано тоже.