|
В основании пирамиды PABCD лежит равнобедренная трапеция с острым углом 45°. Боковые грани РАВ и РСD перпендикулярны основанию пирамиды. а) Докажите, что плоскости РАВ и PCD перпендикулярны. б) Найдите площадь боковой поверхности пирамиды, если известно, что ВС=6, АD=12, а объем пирамиды равен 27.
Как вообразить боковые грани такой пирамиды? Где находится её вершина?Нарисуйте для начала на листе бумаги равнобедренную трапецию: Представим, что мы видим пирамиду сверху. Положите рёбра ладоней
на стороны АВ и DC. Ладони перпендикулярны нарисованной трапеции.
Это и есть боковые грани пирамиды. Пересеките их, соединив ладони.
Увидели ли Вы, по какой прямой пересекаются боковые грани?
Представим, что мы видим пирамиду сверху. Положите рёбра ладоней
на стороны АВ и DC. Ладони перпендикулярны нарисованной трапеции.
Это и есть боковые грани пирамиды. Пересеките их, соединив ладони.
Увидели ли Вы, по какой прямой пересекаются боковые грани?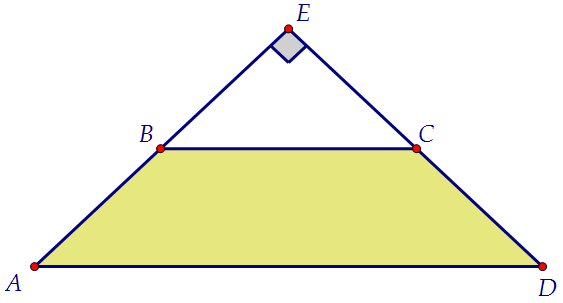 Продлите боковые стороны АВ и DC трапеции и в полученную точку Е
вбейте не до конца гвоздь. Шляпка гвоздя - это вершина пирамиды Р.Найдём угол между ладонями - боковыми гранями пирамиды.
Ребро двугранного угла - это и есть вбитый не до конца гвоздь.
Оно перпендикулярно плоскости трапеции, а значит, и боковым
сторонам трапеции. Угол АЕD - линейный угол двугранного угла.
Он равен 90°. Значит, боковые грани пирамиды перпендикулярны.
Чтобы найти площадь боковой поверхности пирамиды, надо сложить
площади четырёх боковых граней, каждая из которых - треугольник.
Для начала раскрутим данную по условию равнобедренную трапецию:
Продлите боковые стороны АВ и DC трапеции и в полученную точку Е
вбейте не до конца гвоздь. Шляпка гвоздя - это вершина пирамиды Р.Найдём угол между ладонями - боковыми гранями пирамиды.
Ребро двугранного угла - это и есть вбитый не до конца гвоздь.
Оно перпендикулярно плоскости трапеции, а значит, и боковым
сторонам трапеции. Угол АЕD - линейный угол двугранного угла.
Он равен 90°. Значит, боковые грани пирамиды перпендикулярны.
Чтобы найти площадь боковой поверхности пирамиды, надо сложить
площади четырёх боковых граней, каждая из которых - треугольник.
Для начала раскрутим данную по условию равнобедренную трапецию: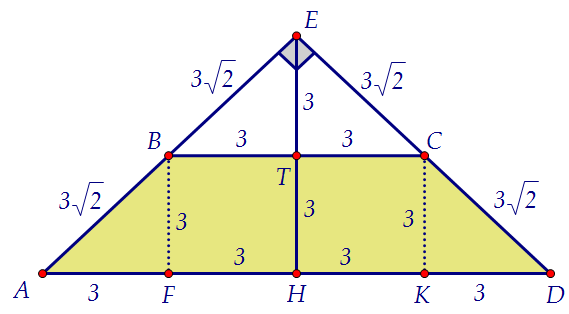 Площадь трапеции S = 9 · 3 = 27. Объём пирамиды тоже равен 27.
Значит, высота пирамиды РЕ (длина вбитого гвоздя) равна 3.
У левой и правой боковых граней основания известны, высота 3.
Площадь трапеции S = 9 · 3 = 27. Объём пирамиды тоже равен 27.
Значит, высота пирамиды РЕ (длина вбитого гвоздя) равна 3.
У левой и правой боковых граней основания известны, высота 3.
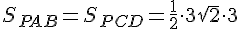
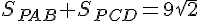 У дальней грани основание 6, а высота - расстояние от Р до ВС.
Это расстояние находим из прямоугольного треугольника РЕТ:
У дальней грани основание 6, а высота - расстояние от Р до ВС.
Это расстояние находим из прямоугольного треугольника РЕТ:
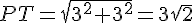 У ближней грани основание 12, а высота - расстояние от Р до AD.
Это расстояние находим из прямоугольного треугольника РЕН:
У ближней грани основание 12, а высота - расстояние от Р до AD.
Это расстояние находим из прямоугольного треугольника РЕН:
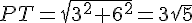 Найдём теперь площади дальней и передней граней:
Найдём теперь площади дальней и передней граней:
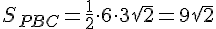
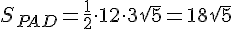 Складывая получившиеся результаты, получим ответ:
Складывая получившиеся результаты, получим ответ:
)  Автор: Ольга Себедаш Просмотров: 10683
|

 Представим, что мы видим пирамиду сверху. Положите рёбра ладоней
на стороны АВ и DC. Ладони перпендикулярны нарисованной трапеции.
Это и есть боковые грани пирамиды. Пересеките их, соединив ладони.
Увидели ли Вы, по какой прямой пересекаются боковые грани?
Представим, что мы видим пирамиду сверху. Положите рёбра ладоней
на стороны АВ и DC. Ладони перпендикулярны нарисованной трапеции.
Это и есть боковые грани пирамиды. Пересеките их, соединив ладони.
Увидели ли Вы, по какой прямой пересекаются боковые грани? Продлите боковые стороны АВ и DC трапеции и в полученную точку Е
вбейте не до конца гвоздь. Шляпка гвоздя - это вершина пирамиды Р.Найдём угол между ладонями - боковыми гранями пирамиды.
Ребро двугранного угла - это и есть вбитый не до конца гвоздь.
Оно перпендикулярно плоскости трапеции, а значит, и боковым
сторонам трапеции. Угол АЕD - линейный угол двугранного угла.
Он равен 90°. Значит, боковые грани пирамиды перпендикулярны.
Чтобы найти площадь боковой поверхности пирамиды, надо сложить
площади четырёх боковых граней, каждая из которых - треугольник.
Для начала раскрутим данную по условию равнобедренную трапецию:
Продлите боковые стороны АВ и DC трапеции и в полученную точку Е
вбейте не до конца гвоздь. Шляпка гвоздя - это вершина пирамиды Р.Найдём угол между ладонями - боковыми гранями пирамиды.
Ребро двугранного угла - это и есть вбитый не до конца гвоздь.
Оно перпендикулярно плоскости трапеции, а значит, и боковым
сторонам трапеции. Угол АЕD - линейный угол двугранного угла.
Он равен 90°. Значит, боковые грани пирамиды перпендикулярны.
Чтобы найти площадь боковой поверхности пирамиды, надо сложить
площади четырёх боковых граней, каждая из которых - треугольник.
Для начала раскрутим данную по условию равнобедренную трапецию: Площадь трапеции S = 9 · 3 = 27. Объём пирамиды тоже равен 27.
Значит, высота пирамиды РЕ (длина вбитого гвоздя) равна 3.
У левой и правой боковых граней основания известны, высота 3.
Площадь трапеции S = 9 · 3 = 27. Объём пирамиды тоже равен 27.
Значит, высота пирамиды РЕ (длина вбитого гвоздя) равна 3.
У левой и правой боковых граней основания известны, высота 3.