Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В кубе АВСDA₁B₁C₁D₁ точка N – середина ребра ВС, точка М лежит на ребре АВ так,
что МВ = 2·МА. Плоскость, проходящая через точки М и N параллельно прямой ВD₁,
пересекает ребро DD₁ в точке К.
б) Найдите расстояние от точки D₁ до прямой МN, если известно, что ребро куба равно 12.

Основная идея решения простая. Опустим перпендикуляр из точки D₁ на MN.



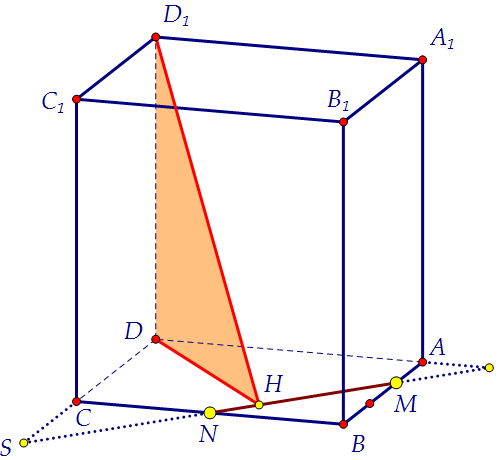Проекцией наклонной D1H на плоскость ABCD является отрезок DH.
По теореме о трёх перпендикулярах проекция перпендикулярна MN.
Таким образом, достаточно найти сначала длину отрезка DH.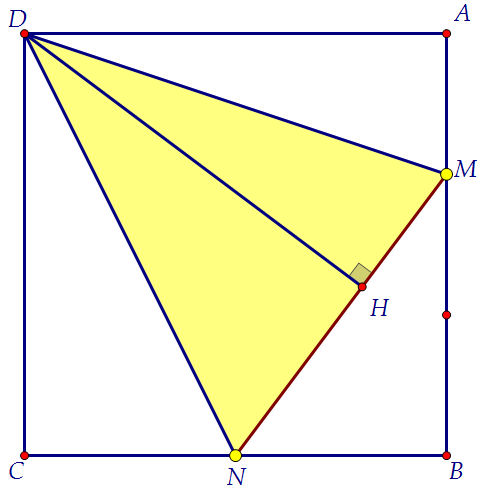



Для поиска высоты DH треугольника DMN найдём его площадь и длину MN.



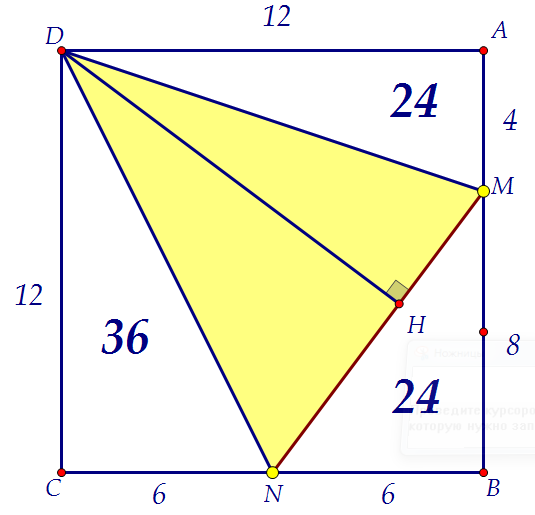S_DMN = 144 - 36 - 24 - 24 = 60; MN = 10, DH = 12.

Итак, длина проекции известна. D₁H - гипотенуза равнобедренного
прямоугольного треугольника, катеты которого равны по 12.

Ответ: 12√2

Автор: Ольга Себедаш             Просмотров: 4378