|
Найдите все значения параметра а, при которых уравнение имеет ровно три различных действительных корня.
^2-{2a}\cdot{\frac{x-1}{x^2+1}}+a^2-0,25=0) Сделав очевидную замену и применив теорему Виета, легко получим, что
исходное уравнение равносильно совокупности двух новых уравнений:
 
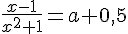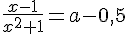Очевидно, что общих корней уравнения не имеют (иначе а - 0,5 = а + 0,5).
На положительный знаменатель запросто умножим оба уравнения:
x^2-x+(a+1,5)=0) x^2-x+(a+0,5)=0)
1) Если а = -0,5, то первое уравнение имеет один корень. А что со вторым?Оно превращается в уравнение -х2 - x = 0 и имеет два корня. Условие выполнено, число -0,5 пойдёт в ответ.
2) Если а = 0,5, то второе уравнение имеет один корень. А что с первым?Оно превращается в уравнение х2 - x + 2 = 0 и не имеет корней. Условие НЕ выполнено, число 0,5 НЕ пойдёт в ответ.
3) Если а ≠ ±0,5, то оба уравнения являются квадратными. В каком случае
они в совокупности имеют три корня (учитывая, что совпасть корни не могут)?
Ответ на этот вопрос прост. Один из дискриминантов должен быть равен нулю, второй при этом должен быть положительным. Найдём оба дискриминанта.D1 = 1 - 4(a + 0,5)(a + 1,5) = -2(2a2 + 4a + 1).
D2 = 1 - 4(a + 0,5)(a - 0,5) = -2(2a2 - 1).
Нули первого дискриминанта обозначим a1 и a2, нули второго - a3 и a4.
   
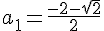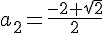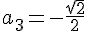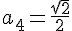Расположим эти точки на оси. При этом неплохо бы сравнить a2 и a3.
Первый дискриминант положителен на интервале (a1, a2).
Этому интервалу принадлежит точка a3, обращающая в ноль D2.
Второй дискриминант положителен на интервале (a3, a4).
Этому интервалу принадлежит точка a2, обращающая в ноль D1.
Таким образом точки a2 и a3 тоже берём в ответ.Ответ: 0,5√2 - 1; -0,5√2; -0,5 Автор: Ольга Себедаш Просмотров: 8440
|
