|
Автофургон грузоподъемностью 339 кг перевозит ящики с виноградом и яблоками.
Вес и стоимость ящика с виноградом составляют 15 кг и 10 у.е., ящика с яблоками –
27 кг и 8 у.е. соответственно. Известно, что количество загруженных на автофургон
ящиков с виноградом составляет не более 70% от количества загруженных ящиков
с яблоками. Определите наибольшую возможную суммарную стоимость всех ящиков с виноградом и яблоками, перевозимых автофургоном при данных условиях.
Обозначив число ящиков с виноградом через х, а число ящиков с яблоками через y,сформулируем (запишем в виде неравенств) основные условия задачи: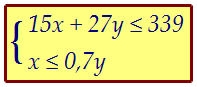 Первое из них поделим на три, получим 5x + 9y ≤ 113. Сделаем первый вывод:
Число ящиков с яблоками не может превышать 12. Иначе говоря, y ≤ 12.
Что требуется найти? Максимальное значение выражения 10x + 8y.
Займёмся перебором вариантов, удовлетворяющих условиям задачи.
1) Пусть y = 12, x = 1. Тогда 10·1 + 8·12 = 106
2) Пусть y = 11, x = 2. Тогда 10·2 + 8·11 = 108
3) Пусть y = 10, x = 4. Тогда 10·4 + 8·10 = 120
4) Пусть y = 9, x = 6. Тогда 10·6 + 8·9 = 132
Если y ≤ 8, то для выполнения второго условия задачи (x ≤ 0,7y) потребуем:x ≤ 0,7·8 = 5,6. Так как х является целым числом, то x ≤ 5.
Если y ≤ 8 и x ≤ 5, то 10x + 8y ≤ 10·5 + 8·8 = 114
Ответ: 132
Первое из них поделим на три, получим 5x + 9y ≤ 113. Сделаем первый вывод:
Число ящиков с яблоками не может превышать 12. Иначе говоря, y ≤ 12.
Что требуется найти? Максимальное значение выражения 10x + 8y.
Займёмся перебором вариантов, удовлетворяющих условиям задачи.
1) Пусть y = 12, x = 1. Тогда 10·1 + 8·12 = 106
2) Пусть y = 11, x = 2. Тогда 10·2 + 8·11 = 108
3) Пусть y = 10, x = 4. Тогда 10·4 + 8·10 = 120
4) Пусть y = 9, x = 6. Тогда 10·6 + 8·9 = 132
Если y ≤ 8, то для выполнения второго условия задачи (x ≤ 0,7y) потребуем:x ≤ 0,7·8 = 5,6. Так как х является целым числом, то x ≤ 5.
Если y ≤ 8 и x ≤ 5, то 10x + 8y ≤ 10·5 + 8·8 = 114
Ответ: 132 Автор: Ольга Себедаш Просмотров: 6041
|

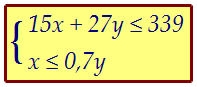 Первое из них поделим на три, получим 5x + 9y ≤ 113. Сделаем первый вывод:
Число ящиков с яблоками не может превышать 12. Иначе говоря, y ≤ 12.
Что требуется найти? Максимальное значение выражения 10x + 8y.
Займёмся перебором вариантов, удовлетворяющих условиям задачи.
1) Пусть y = 12, x = 1. Тогда 10·1 + 8·12 = 106
2) Пусть y = 11, x = 2. Тогда 10·2 + 8·11 = 108
3) Пусть y = 10, x = 4. Тогда 10·4 + 8·10 = 120
4) Пусть y = 9, x = 6. Тогда 10·6 + 8·9 = 132
Если y ≤ 8, то для выполнения второго условия задачи (x ≤ 0,7y) потребуем:x ≤ 0,7·8 = 5,6. Так как х является целым числом, то x ≤ 5.
Если y ≤ 8 и x ≤ 5, то 10x + 8y ≤ 10·5 + 8·8 = 114
Ответ: 132
Первое из них поделим на три, получим 5x + 9y ≤ 113. Сделаем первый вывод:
Число ящиков с яблоками не может превышать 12. Иначе говоря, y ≤ 12.
Что требуется найти? Максимальное значение выражения 10x + 8y.
Займёмся перебором вариантов, удовлетворяющих условиям задачи.
1) Пусть y = 12, x = 1. Тогда 10·1 + 8·12 = 106
2) Пусть y = 11, x = 2. Тогда 10·2 + 8·11 = 108
3) Пусть y = 10, x = 4. Тогда 10·4 + 8·10 = 120
4) Пусть y = 9, x = 6. Тогда 10·6 + 8·9 = 132
Если y ≤ 8, то для выполнения второго условия задачи (x ≤ 0,7y) потребуем:x ≤ 0,7·8 = 5,6. Так как х является целым числом, то x ≤ 5.
Если y ≤ 8 и x ≤ 5, то 10x + 8y ≤ 10·5 + 8·8 = 114
Ответ: 132